You probably came across the floating-point precision formats FP16 and FP32 in GPU specs or in a deep learning application like when training Stable Diffusion with DreamBooth, but did you ever wonder what they mean? Or why do some applications prefer one over the other?
As we all know, computers understand numbers – and pretty much everything else – expressed in the binary number system. Yet, there is no one formula to encode all types of numbers from one number system to another, especially when it comes to floating point numbers.
If you want to encode integers, there are two things you must worry about: the magnitude (informally, the digits) and the sign of the integer. So, when you hear INT8 – which means 8 bits are used to encode an integer, one bit is used to determine the sign of the integer, and the other seven are used to encode the magnitude of our integer.
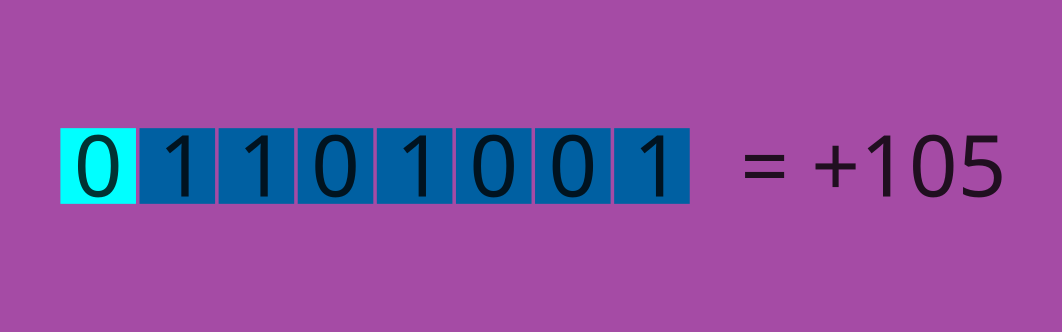
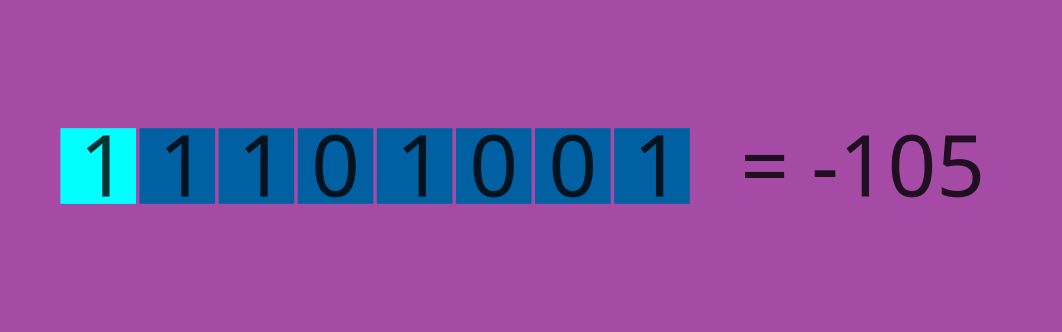
Here you can speculate that the only hindrance is the value of the integer; if your integers are big, you need to use a format with a wider range.
When it comes to floating-point numbers, things get a little more interesting; we have three sets of bits to represent a floating-point number: the sign (always takes one bit), the exponent (or the magnitude; this tells how big the number is), and the mantissa (the precision, this tells how precise or how many digits the number has). The difference between floating point number formats is how many bits are devoted to the exponent and how many are devoted to the mantissa.
FP32
The standard FP32 format is supported by almost any modern Processing Unit, and normally FP32 numbers are referred to as single-precision floating points. This format is used in scientific calculations that don’t require a great emphasis on precision; also, it has been used in AI/DL applications for quite a while.
FP32 precision format bits are divided as follows:
- 1 bit for the sign of the number.
- 8 bits for the exponent, or the magnitude.
- 23 bits for the mantissa or the fraction.
FP32 Range:
Every format has a range of numbers that can be represented with, and with FP32, one can represent numbers of the magnitude of order 10^38, with ~7-9 significant decimal digits.

When do we use FP32 precision?
- Any scientific computations which don’t require more than 6 significant decimal digits.
- In neural networks, this is the default format to represent most network weights, biases, and activation, in short, most parameters.
Software and Hardware Compatibility
FP32 is supported by any CPU and GPU used nowadays; it is represented in popular programming languages by the float type, such as in C and C++. You can also use it in TensorFlow and PyTorch as tf.float32 and torch.float/torch.float32 respectively.
FP16
In contrast to FP32, and as the number 16 suggests, a number represented by FP16 format is called a half-precision floating point number.
FP16 is mainly used in DL applications as of late because FP16 takes half the memory, and theoretically, it takes less time in calculations than FP32. This comes with a significant loss in the range that FP16 covers and the precision it can actually hold.
FP16 precision format bits are divided as follows:
- 1 bit for the sign, as always.
- 5 bits for the exponent or the magnitude.
- 10 bits for the precision or the fraction.
Range:
The representable range for FP16 is in the order of ~10^-8 to ~65504 with 4 significant decimal digits.

When to Use FP16?
It is mostly used in deep learning applications, where the needed range of numbers is relatively small, also the is no demand for precision.
Software and Hardware Compatibility
FP16 is supported by a handful of modern GPUs; because there is a move to use FP16 instead of FP32 in most DL applications, also FP16 is supported by TensorFlow by using the type tf.float16 and in PyTorch by using the type torch.float16 or torch.half.
In other programming languages, the type short float is often used to encode a half-precision floating point number.
FP16 vs FP32
Both of these formats are best suited for their usages, but there are some points to take into account when you want to choose one of these:
Range
The range is essential for choosing which format to use; for example, if you are working with integers of order a few 1000s, it is not reasonable to use INT8; because its range is bounded by 255.
INT32 isn’t reasonable either; because you are not going to use many of these bits, and this is a waste of memory.
Precision
Naturally, precision increases with the bits increment. This means if you need precise results, you should use formats with more precision bits, but this will increase space and time requirements of the calculations.
Using FP16 instead of FP32 in deep learning proved helpful in decreasing the time and space needed for training the models without much loss in the performance of these models.
This transition prevents overfitting to some extent; if the models’ parameters are highly adjustable, this opens a window for overfitting to your training data.
In contrast, FP16 opens a tiny window for overflow and underflow, where you try to compute numbers out of the representable range. Or with unnoticeable differences with regard to this format.
The caveat in DL networks is that the range matters but not the precision, which lead to the invention of BFLOAT16 – short for Google’s Brain float 16. Just an FP32 with it’s precision truncated to leave it with 16 bits.
BFLOAT16 combines the best of both worlds; it has the range of FP32 by using 8 bits as the exponent and 7 bits as the precision part. This makes it possible to represent the whole range of FP32 with BFLOAT16, but with little precision. i.e., you can compare two numbers with a meaningful difference in magnitude, but the same can’t be said for two close numbers (underflow), which isn’t a big issue in DL applications.
A great example to mentalize the difference which is related to computer vision; consider a robotic hand that helps clean valuable pieces; precision is essential in this case. This is opposed to another hand that helps in cutting metals in a factory, which requires fast production rate.
In the example with the first hand, it is plausible to FP32 instead of FP16, which is more suitable to the nature of the industrial-level metal cutting machine!
Conclusion
In this article, we discussed FP16 and FP32, and we compared them with each other; we knew that if we favor speed over precision, we should use a format with fewer bits and vice versa.






